< К оглавлению

В настоящем выпуске мы продолжим рассмотрение общих свойств режимов шифрования различных типов. Рассмотрим чуть подробнее проблему последнего блока. Эта проблема заключается в том, что шифруемые массивы данных могут иметь произвольный размер, и, естественно, содержать нецелое число блоков, как показано ниже на рисунке 1:

Рис. 1. Шифруемый массив данных может состоять из нецелого числа блоков.

С другой стороны, блочному криптографическому преобразованию E_K, а значит и зашифрованию в одном из режимов блочного типа, выполняемому в соответствии со следующим уравнением

может быть подвергнут только полный блок данных. Именно такой блок, модифицированный значением рандомизирующей функции f, является операндом криптографического преобразования E_K, которое по определению оперирует только блоками данных фиксированного размера. В результате появляются две следующие проблемы технического характера:

1. Чем и как дополнять неполный последний блок шифруемого массива данных до полного размера.
2. Где и как хранить в шифротексте информацию об истинном размере последнего блока открытых данных - после дополнения и зашифрования она естественным образом теряется.

Рассмотрим эти проблемы подробнее. Способ дополнения последнего блока шифруемых данных имеет определенное значение для стойкости шифра. Если в каком-либо конкретном случае криптоаналитик сможет определить или оценить добавленный код с вероятностью успеха, большей чем при простом угадывании, то соответственно повышаются и его шансы успешно определить последний блок шифруемых данных. Следовательно, для обеспечения максимальной стойкости желательно сохранять у противника полную неопределенность относительно добавленного кода. В соответствии с принятом в криптографии принципом Кирхгофа сам способ получения кода при этом может быть ему известен.

С учетом сказанного выше наилучшим решением проблемы является дополнение неполного блока случайными данными, выработанными генератором истинно случайных чисел. Однако это не всегда приемлемо по экономическим соображениям, так как такой генератор может быть реализован либо на основе специального аппаратного блока, получающего случайные биты с помощью "шумящих" электронных приборов, обычно - шумящих диодов и транзисторов, или от внешних по отношению к компьютеру физических процессов, либо без дополнительных устройств но с участием в процессе выработки случайных данных человека. Первый подход приводит к появлению в компьютере дополнительного аппаратного устройства, и, следовательно, к удорожанию системы; второй не может обеспечить достаточной производительности получения случайных данных, так как быстродействие человека как звена такой системы крайне низко. Следовательно, остается использование детерминированных решений, основанных на выработке дополняющего кода с помощью некоторой функции или алгоритма.

Необходимо отметить, что добавляемый код должен вырабатываться каким-либо явным способом, хотя формально есть возможность избежать этого, а раз есть возможность, то может появиться и соблазн ее использовать. Конечно, алгоритм требует, чтобы шифруемый блок был полным, то есть чтобы все двоичные разряды операнда криптографического преобразования приняли какие-либо конкретные значения. Однако для программной и аппаратной реализации это выполняется автоматически, ибо участки машинной памяти или регистры, куда заносится блок данных, подлежащий преобразованию, по определению имеют необходимый размер. Суть "пассивного" подхода заключается в том, чтобы не предпринимать никаких специальных действий по заполнению участка памяти, соответствующего отсутствующей части последнего блока. Понятно, что в этом случае он будет содержать данные, оставшиеся там от предыдущего использования, что собственно, и является возможным источником проблем - таким образом в шифруемый массив могут попасть данные от другого секретного сообщения, что неприемлемо для серьезных систем обеспечения секретности.

Простейший подход к дополнению "хвоста" заключается в том, чтобы добавлять к нему отрезок фиксированных данных подходящего размера. Однако, как отмечено выше, это может позволить криптоаналитику определить значение последнего блока, так как в этом случае часть полного блока открытого текста будет фактически известна ему, и для определения оставшейся части потребуется перебор по меньшему пространству. Конечно, такая возможность актуальна, если противнику доступен анализ на основе произвольного выбранного открытого текста.

В общем случае для решения проблемы может быть использована функция зависящая от предыдущих открытых и зашифрованных блоков данных:

,
,

где h_l(...) - некоторая функция, возвращающая в качестве результата l-битовый отрезок данных, выработанный из аргументов. При этом выполняется следующее соотношение для размеров блоков:

.
В рассмотренном выше простейшем частном случае = const.

Для обеспечения необходимой стойкости шифра, то есть для создания у криптоаналитика максимальной неопределенности относительно дополняющего кода, его следует вырабатывать из данных, недоступных противнику, т.е. не известных априорно, не в ходящих в шифротекст и не связанных с блоками шифротекста какими-либо простыми соотношениями. По этой причине идея дополнять "хвосты" кодом из какого-либо блока шифротекста ненамного лучше идеи использовать для этого фиксированный код. Использовать для дополнения какой-либо блок открытого текста тоже нежелательно, так как при этом один и тот же фрагмент исходных данных будет присутствовать в шифруемых данных дважды, что чисто теоретически может дать в руки аналитика дополнительную возможность для анализа. Хорошим решением проблемы будет дополнение неполного блока результатом криптографического преобразования, не встречающегося в явном виде в шифротексте, что потребует выполнения одного "лишнего" цикла преобразования. По сути это является генерацией псевдослучайного элемента данных, т.е. аналогом выработки случайного числа. Например, в качестве дополняющего кода можно взять результат зашифрования предпоследнего блока шифротекста:

,

где через P_l(X) обозначается какой-либо способ выбрать фрагмент кода размером l бит из блока кода X большего или равного размера,

Другая, техническая сторона проблемы последнего блока заключается в том, что в полученном блоке шифротекста все разряды являются значащими, даже если соответствующий исходный блок был неполным. Иными словами, они необходимы для выполнения процедуры расшифрования, и поэтому не могут быть отброшены и должны обязательно присутствовать в шифротексте. Простейшее, но не единственное следствие из этого заключается в том, что размер шифротекста увеличивается по сравнению с размером открытого текста до ближайшего кратного размера блока. Кроме того, при дополнении неполного блока информация о его истинном размере теряется - ведь два имеющих разные размеры блока, один из которых является частью другого, могут быть дополнены обсуждаемыми выше способами так, что получатся одинаковые блоки. Следовательно, в этом случае результат расшифрования потенциально неоднозначен и для выбора нужного варианта из нескольких возможных необходима информация о длине блока, которая, очевидно, должна храниться или передаваться вместе с зашифрованными данными. В общем случае, если отсутствуют априорные условия относительно размера или содержимого открытых данных, то размер шифротекста всегда больше размера открытых данных. В частности, если исходные данные состоят из целого числа блоков криптоалгоритма, все равно придется добавить еще один блок, и шифротекст будет содержать на один полный блок больше, что может оказаться неприемлемым для реальной системы обеспечения секретности.

Для потоковых режимов шифрования проблема последнего неполного блока отсутствует. Конечно, в уравнении зашифрования в режимах этого типа

T'_i = T_i °  E_K(f(T₁,T₂,...,T_i-1,T'₁,T'₂,...,T'_i-1,S))

подвыражение E_K(f(T₁,T₂,...,T_i-1,T'₁,T'₂,...,T'_i-1,S)) является блоком полного размера. Однако операции модификации "° " практически всегда достаточно проста и ее можно определить и для неполных блоков, в этом случае для модификации будет реально использована только часть правого операнда:

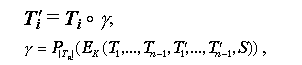
где P_l(X) определено в указанном выше смысле. Простые бинарные операции аддитивного типа легко переопределить для любого размера операндов. В контексте данной проблемы желательно, чтобы операция модификации шифруемого блока обладала еще одним свойством: если шифруемый блок состоит из значащей (неполной) и балластной (добавленной) частей, то фрагмент результата зашифрования, соответствующий значащей части исходного блока, не должен зависеть от добавленной части. Иными словами, если

X^* = (X,X⁺), Y^* = (Y,Y⁺), Z^* = (Z,Z⁺) и Z^* = X^* °  Y^*, где

|X| = |Y| = |Z| и |X⁺| = |Y⁺| = |Z⁺|,

то Z не должен зависеть от X⁺ и Y⁺. Если данное свойство выполняется для операции гаммирования, можно не беспокоиться о том, какое значение приняла неиспользованная часть шифруемого блока. При любом "мусоре", содержащемся в ней, в значащих разрядах результата будет одно и то же значение, которое, естественно, и будет "правильным". Указанное свойство выполняется, если используется операция аддитивного типа и значащей частью блока является его младшая часть. Операция побитового исключающего ИЛИ и здесь имеет свои преимущества, так как в случае ее использования двоичные разряды результата зависят только от соответствующих двоичных разрядов операндов и не зависят от их других разрядов, в силу чего указанное свойство выполняется автоматически, какое бы место значащая часть ни занимала внутри блока. Это, однако, не снимает еще одной проблемы, касающейся совместимости реализаций шифров на различных аппаратных платформах. Дело в том, что неполный блок может быть по-разному размещен внутри полного, - это зависит от архитектуры процессора. Так, на популярных процессорах линии Intel x86 заполнение нового блока начинается с его младших разрядов, а во многих архитектурах, таких, например, как HP PA, наоборот, со старших. Если алгоритм шифрования сформулирован в терминах целых чисел, по разрядности превышающих наименьшую адресуемую единицу машинных данных (обычно это байт), то, если не принять специальных мер, информацию, зашифрованную на компьютере одной архитектуры, будет невозможно правильно расшифровать на компьютере другой. Впрочем, это известная проблема "порядка байт", она существует в более широком, нежели криптография, контексте совместимости по данным программ для различных аппаратных платформ, и, естественно, в компьютерной криптографии тоже актуальна. Поскольку проблема не относится непосредственно к изучаемому вопросу, мы не будем ее рассматривать, отметим лишь, что проблема не представляет серьезной трудности и пути ее решения хорошо известны.

Теперь вернемся к проблеме увеличения размера шифротекста по сравнению с открытым текстом, неизбежного в блочном режиме при использовании простого дополнения блока. Как уже отмечалось выше, такое увеличение не всегда приемлемо, и чтобы его избежать, были разработаны специальные подходы, позволяющие, организовать шифрование таким образом, чтобы размер шифротекста был равен размеру открытого текста и в блочных режимах. Ниже мы остановимся на двух самых популярных из них:

Шифрование "хвоста" в потоковом режиме.

Поскольку проблема неполного блока неактуальна для потоковых режимов, одним из способов ее решения является использование такого режима для шифрования последнего блока: все полные блоки шифруются в блочном режиме, а последний, неполный - в потоковом. Такой подход позволяет соединить в одной схеме шифрования преимущества обоих типов режимов. В этом случае для выработки гаммы для шифрования неполного блока наиболее всего удобно использовать предпоследний блок шифротекста, то есть результат зашифрования последнего полного блока исходного текста. В этом случае уравнения за- и расшифрования последнего блока будут следующими:

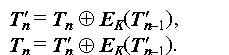
Сокрытие или "кража" "лишнего" шифротекста.

Этот оригинальный способ решения проблемы позволяет не хранить "лишний" шифротекст, получающийся при зашифровании дополненного блока, а "спрятать" его в результатах шифрования. Он предполагает, что два последних блока открытого текста в шифротексте меняются местами. Ниже даны уравнения за- и расшифрования двух последних блоков при использовании данного подхода в режиме простой замены. Они остаются в силе для любого другого блочного режима, если под T_i понимать блоки исходных данных, уже модифицированные в соответствии с условиями выбранного режима. Иными словами, для всех режимов блочного типа кроме режима простой замены в следующих ниже уравнениях надо заменить T_i на T_i   f(T₁,T₂,...,T_i-1,T'₁,T'₂,...,T'_i-1,S). В этих уравнениях через M обозначен размер последнего шифруемого блока, который по условию не должен превышать размер блока криптоалгоритма:

Зашифрование:

T'_n = Hi_M(E_K(T_n-1)),

T^* = Lo_N-M(E_K(T_n-1)),

T'_n-1 = E_K(T_n || T^*).

Расшифрование:

T_n = Hi_M(D_K(T'_n-1)),

T^* = Lo_N-M(D_K(T'_n-1)),

T_n-1 = D_K(T'_n || T^*).

Понятно, что при этом размер последнего блока шифротекста получается равным размеру последнего блока исходных данных: |T'_n| = |T_n| = M. Ясно, что в предельном случае при M = N все сводится к банальной перестановке двух последних блоков, однако тем не менее приведенные выше уравнения остаются корректными.

Приведенные выше уравнения шифрования наиболее удобны для машинных архитектур, в которых заполнение слова начинается со старших его байтов. Можно реализовать этот подход и по-другому - способом, более удобным для архитектуры Intel и ей подобным, при этом уравнения шифрования будут следующими:

Зашифрование:

T'_n = Lo_M(E_K(T_n-1)),

T^* = Hi_N-M(E_K(T_n-1)),

T'_n-1 = E_K(T^* || T_n).

Расшифрование:

T_n = Lo_M(D_K(T'_n-1)),

T^* = Hi_N-M(D_K(T'_n-1)),

T_n-1 = D_K(T^* || T'_n).

Следует отметить, что оба описанных выше способа решения проблемы последнего блока существенным образом используют условие, что шифруемые данные содержат не менее одного полного блока и, таким образом, не работают на сверхкоротких сообщениях, размер которых меньше размера блока криптоалгоритма - там нужно искать другие подходы.

Еще один аспект проблемы режимов шифрования заключается в характере распространения ошибок при за- и расшифровании. Очевидно, результат шифрования изменится, если будут изменены шифруемые данные. Естественно, что оценка влияния изменения аргументов на изменения результата криптопреобразования представляет особый интерес для криптоаналитика. Обе задачи оценки распространения ошибок - для за- и расшифрования - связаны между собой. Если криптоаналитику удастся точно оценить распространение ошибок зашифрования, у него появляется возможность модифицировать шифротекст таким образом, чтобы точно, без побочных эффектов вызвать заданные изменения в открытом тексте, полученном после расшифрования. Если аналитику удастся оценить распространение ошибок при расшифровании, у него появляется возможность прогнозировать влияние заданных изменений в шифротексте на открытые данные, полученные после расшифрования, оценивая таким образом возможность их принятия за подлинные.

Ранее проблема распространения ошибок тесно увязывалась с контролем неизменности данных, и ей уделялось большое внимание при проектировании режимов шифрования. Однако, как убедительно показал Г.Симмонс в своих работах по теории аутентификации, секретность и аутентичность в общем случае являются различными свойствами криптографических систем. Это означает, что контроль целостности данных в общем случае должен обеспечиваться независимо от их шифрования. Поэтому в современной криптографии вопросу распространения или нераспространения ошибок не уделяют столь пристального внимания, как раньше.

Характер распространения ошибок в конкретном режиме существенным образом зависит от его рандомизирующей функции f, и в несколько меньшей степени от того, является режим блочным или потоковым. Для конкретного режима шифрования этот характер легко установить, проанализировав уравнения за- и расшифрование. Главное, что нужно принимать во внимание, что если блок данных модифицируется с использованием другого блока, характер изменения которого предсказуем, то характер изменения модифицированного блока также предсказуем, и наоборот. Если же измененный блок подвергается преобразованию по блочному криптографическому алгоритму, то характер изменения результата преобразования принципиально непредсказуем для аналитика, что следует из условия его стойкости использованного. Пользуясь этими двумя условиями, легко получить оценку характера распространения ошибок для любого режима шифрования.

В заключение скажем, что наряду с двумя основными классами режимов - блочными и потоковыми - существуют более экзотические варианты, в которых каждый блок или группа блоков шифруется на своем ключе. В этом случае нет необходимости в рандомизации, поэтому данные шифруются в режиме простой замены, а основным содержанием такого режима является алгоритм выработки ключа для шифрования очередного блока:

T'_i = E_Ki(T_i),

T_i = D_Ki(T'_i),

K_i = G(K₁,K₂,...,K_i-1,S,K),

Очень желательно (но не обязательно), чтобы при вычислении функции G использовалось криптографическое преобразование E_K. Выполнение последнего условия, однако, приводит к тому, что на шифрование одного блока данных потребует выполнения более одного шага криптопреобразования, что существенно снижает эффективность шифра. По этой причине данные режимы рассматриваются скорее как любопытная теоретическая возможность, нежели как практический вариант.

Вот, собственно, и вся теория, касающаяся режимов шифрования. Следующий выпуск будет посвящен рассмотрению конкретных режимов.

(Продолжение следует)