Информационные технологии, Infused Bytes - архив

30 октября 1998, 00:00 (9527 дней назад, №6065)Заметки о вокселах

(Сергей Зефиров, 30 октября 1998)

Вступление

Слово воксель - voxel - образовано от слова VOlume и аббревиатуры piXEL (pixel, расшифровывается как PICture'S ELement, элемент картины). То есть, переводится как "элемент объемного изображения" или "элемент объема изображения".. Обычно это шар или куб.

Не стоит приписывать пикселу и вокселю равносторонность. Это удобно, не более того. Иногда даже удобнее считать воксель неким параллепипедом - например, в карте высот.

Применения вокселей

Наиболее широкое применение воксели нашли в медицине, в компьютерной томографии, в частности. Изображения с большого количества рентгеновских или ультразвуковых снимков под разными углами (порядка 100-200 снимков) обрабатываются, и создается трехмерный массив плотностей различных участков тканей исследуемого органа. Этот массив представляет собой "объемную картину", элементом которой является воксель.

Второе, более наглядное, применение вокселей - компьютерные игры. В Shadow Warrior с помощью трехмерного массива задается форма оружия, а во всем известных Команчах - ландшафт. И если в Shadow Warrior воксели квадратные, а массив трехмерный, то в Команчах воксели представляют собой параллепипед 1*1*высота_местности, а массив двумерный. Поэтому в Команчах не видно нависающих над берегом моря утесов - такое вот ограничение на представление пространства.

Способы отображения

Двумерные массивы высот отображаются методом плавающего горизонта в комбинации с методом отслеживания лучей (raycasting, не путать с reytracing). Способ чрезвычайно прост:

void cast_ray(int scrx,real x,real y,real dx,real dy) {
   max_height=0;
   for(dist=0;dist<view_depth;dist++) { // ограничение по дальности
      h=fetch_height(x,y);           // взять высоту из карты высот
      scrh=height_to_screen(h,dist); // преобразовать высоту в экранную
      if(scrh>max_height){           // текущий столбец "выше" самого высокого отрисованого
         color=fetch_color(x,y);
         draw_column(scrx,max_height,height,color); // отрисовать видимую часть
         max_height=height;
      }
      x=x+dx;                        // единичный шаг вперед, вдоль луча
      y=y+dy;
   }
}

Обычно значения высот отрисованных столбцов запоминаются, для того, чтобы можно было отрисовать выступающие над ландшафтом объекты.

Что касается трехмерных массивов, то здесь все зависит от специфики приложения, поэтому методов их отображения существует несколько:

Честная трассировка лучей.
Традиционный "лобовой" метод, с которым все борются.
Построение изоповерхности.
Перед отображением объем переводится в набор плоскостей, описывающих "поверхности" объема.
Один из методов пакета VolVis.
Не очень хорош (с моей точки зрения) при отображении объемов с полупрозрачными участками.
Отображение через преобразование Фурье.
Метод основан на теореме об обратном преобразовании двумерного среза преобразования Фурье. Вкратце смысл ее таков: если вычислить прямое преобразование Фурье для объема N*N*N, затем взять его срез плоскостью P, проходящей через центр объема, затем произвести обратное преобразование Фурье, то результат будет представлять собой двумерный массив, с элементами, содержащими сумму элементов, соответствующих трассировке объема лучами, перпендикулярными P.
Подробнее - здесь .
Требует N**3 памяти под комплексные числа, сложность оценивается как O(N**2*log(N)).
Существенным недостатком является отсутствие отсечения скрытых деталей - результаты работы алгоритма очень похожи на рентгеновские снимки.
"Пропуск пространства" - Space Leaping
Предобработкой производится выделение и объединение пустых участков пространства, и во время трассировки лучей такие участки просто пропускаются.
Включает в себя трассировку лучей.
Отображение с помощью фильтра
Для каждого отображаемого вокселя определяется экранная координата его центра, а затем параметры вокселя "разбрасываются" по соседним пикселам с ипользованием некоторого фильтра. Коэффициенты фильтра зависит только от желаемого качества.
Чаще всего используемый фильтр - считать проекцию воксела квадратом с однородными параметрами (Shadow Warrior).

Octree для хранения данных об объеме

Два способа хранения таких данных я уже упомянул выше: массив N*N*N и карта высот. Хочется добавить еще один способ, а именно octree (восьмидерево;). От двоичного дерева его отличает способ деления пространства - сразу на восемь равных частей, с линейными размерами вдвое меньше, чем у предка.

Чем интересен такой способ хранения данных? Тем, что при добавлении в восьмидерево единичного объема автоматически обходятся пустые участки. Вот часть кода обработки восьмидерева в качестве иллюстрации:

// _subdivide отыскивает необходимый элемент восьмидерева,
// создавая отсутствующие элементы дерева по необходимости
   static hnode* _subdivide(hnode*p,livec3*center,longint x,longint y,longint z,int step) {
   longint hs=p->size;
   int index=0;
   hnode *child;
   livec3 ncenter;  // новые координаты центра
   if(x>=(*center)[X_DIM]) index|=X_SUB; // Вычисление индекса потомка
   if(y>=(*center)[Y_DIM]) index|=Y_SUB; // двоичным делением по трем
   if(z>=(*center)[Z_DIM]) index|=Z_SUB; // координатам
   child=p->childs[index];
   if(!child) { // Нет необходимого потомка на этом уровне
      child=new_node(); if(!child) return 0; // создать потомка в случае отсутствия
      init_pointers(child,p);
      p->childs[index]=child; child->parent=p; child->size=hs/2;
   }
   if(hs<2) return child; // Если деление дальше не нужно
                          // (потомок, содержащий (x,y,z) наименьшего размера найден)
   ncenter[X_DIM]=(*center)[X_DIM];
   ncenter[Y_DIM]=(*center)[Y_DIM];
   ncenter[Z_DIM]=(*center)[Z_DIM];
   hs/=2;
// Следует добавить, что центром корневого элемента является точка (0,0,0)
   if(index&X_SUB) ncenter[X_DIM]+=hs; else ncenter[X_DIM]-=hs;
   if(index&Y_SUB) ncenter[Y_DIM]+=hs; else ncenter[Y_DIM]-=hs;
   if(index&Z_SUB) ncenter[Z_DIM]+=hs; else ncenter[Z_DIM]-=hs;
   return _subdivide(child,&ncenter,x,y,z,step+1);
} /* _subdivide */

Если некоторый объем "пуст" - то есть, имеет стандартные параметры - то ссылка на него просто не появляется.

Таким образом, пропуск пустых пространств неявно реализован в восьмидереве.

Перспективная проекция восьмидерева

При перспективной проекции на разных расстояниях от камеры частота выборки элементов изображения различна.

Например, на расстоянии (z координата пространства камеры) в диапазоне 0.25..0.5 фокусного расстояния единичный объем будет выбран четыре раза. (x_scr=x_cam*z_focus/z_cam, z_cam/z_focus=C=0.25..0.5, отсюда x_cam(x_scr)=x_scr*C, x_cam(x_scr+1)-x_cam(x_scr)=C=0.25..0.5, то есть, элемент единичного линейного размера будет отображен размером в два-четыре пиксела)

На расстоянии от одного до двух фокусных расстояний элементы единичного объема будут отображены в экранные объекты менее, чем в один пиксел размером. То есть, в одном пикселе будут смешаны до четырех вокселей. На расстоянии от 16 до 32 фокусных в одном пикселе смешаются до 1024 (32*32) вокселей. И чем дальше, тем больше.

Однако, можно попробовать хранить в узлах восьмидерева не только ссылки на потомки, но и обобщенную визуальную информацию о них. Это поможет решить проблему смешивания нескольких вокселей - если на расстоянии, где воксел единичного размера отображается в полпиксела, отображать воксел двойного линейного размера (с усредненными параметрами) то, во-первых, отображается меньше вокселей (вокселей двойного размера в каком-то объеме в восемь раз меньше, чем единичного), а во-вторых мы обходим проблему смешения нескольких вокселей в один пиксел. Этот прием сродни используемому в наложении текстур приему мипмаппинг (mipmapping).

Объединение визуальных параметров потомков

Во-первых, при объединении объемов надо усреднить их цвет. Во-вторых, надо усреднить прозрачность - вероятность искажения проходящего сквозь объем луча света.

Для правильного понимания процесса стоит взглянуть на интеграл отображения от Jim Kajiya:

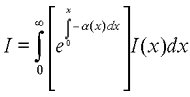Суммарная интенсивность вдоль луча равна сумме интенсивностей в точке луча (I(x)), умноженных на полное затухание вдоль луча (exp(sum(alpha(x)dx))).

Сперва разберемся с прозрачностью, как с более простым случаем.

Действительно, с прозрачностью все лежит на поверхности: общая прозрачность не меняется при изменении знака обхода с 0->x на x->0, поскольку от перемены мест слагаемых сумма не изменяется. Если использовать не логарифмические alpha(x), а a(x)=exp(-alpha(x)), то сумма просто заменяется на умножение. (От перемены мест сомножителей результат не изменяется;)

Итак, вдоль каждой оси координат (отдельно Ox, Oy и Oz) я считаю среднюю прозрачность для стороны кубика:

T(dir)=(T(dir,upleft,forward)*T(dir,upleft,backward)+
    T(dir,downleft,forward)*T(dir,downleft,backward)+
    T(dir,upright,forward)*T(dir,upright,backward)+
    T(dir,downright,forward)*T(dir,downright,backward) )/4;

forward и backward, left и right, up и down - координаты вокселей-потомков. Обе эти переменные зависят от направления dir. Например, для оси Oy forward будет (0,+0,0), backward - (0,-1,0), upleft - (+0,0,+0), downright - (-1,0,-1).

Иными словами, средняя прозрачность для некоторого направления есть среднее арфиметическое суммарных прозрачностей пар вокселей, объединенных по направлению.

Теперь стоит перейти к цвету.

В общем случае, для всех шести сторон кубика-воксела цвет будет различен (как пример - Кубик Рубика). Более того, это же видно из интеграла Kajiya - для разных направлений у интенсивностей I(x) разные множители. Поэтому в структуре, хранящей визуальные параметры воксела присутствует шесть (число измерений * 2) не связанных между собой записей о цвете.

Цвет для определенной стороны (side) считается как взвешенная сумма цветов (для сторон side) четырех пар вокселей, с учетом заслонения прозрачными вокселами. Пример кода (на этот раз псевдокод):

component=0;
traspsum=0;
for(i in (upleft,upright,downleft,downright)) { // перебираем четыре пары
   transparency t=child[i,forward].transparency[side/2],
                tb=child[i,backward].transparency[side/2];
   component+=(child[i,forward].components[side]*t+ // учет заслонения
               child[i,backward].components[side]*(1-t)
              )*(1-t)*(1-tb); // вес - общая непрозрачность
   transpsum+=(1-t)*(1-tb);
}
if(transpsum<1) transpsum=1; // Жизнь без divide by zero
current.components[side]=component/transpsum;

Я еще не рассказал, как во время отображения вычислять прозрачность и цвет разноцветного вокселя. Это чрезвычайно просто: если вектор воксель-камера равен (A,B,C), то прозрачность считается так:

transp=voxel->trnsparency[X_DIR]*abs(A)+
       voxel->trnsparency[Y_DIR]*abs(B)+
       voxel->trnsparency[Z_DIR]*abs(C);
transp/=abs(A)+abs(B)+abs(C);

То есть, как взвешеная сумма прозрачностей по трем направлениям, где веса - площади проекций соответствующих сторон.

Цвет считается похожим образом, только в игру вступает направление взгляда (знак):

comp=voxel->component[X_SIDE+(A<0)]*abs(A)+
     voxel->component[Y_SIDE+(B<0)]*abs(B)+
     voxel->component[Z_SIDE+(C<0)]*abs(C);
comp/=abs(A)+abs(B)+abs(C);

Вот теперь - все. ;)

Теперь можно обсуждать недостатки.

Недостатки воксельной технологии

Стоит начать с самого главного - это неторопливость. Для каждого объема приходится выполнять как минимум одно деление.

Значительный расход памяти: на каждый воксель, вне зависимости от его размера, требуется

6*sizeof(RGB)/*цвет*/+
3*sizeof(byte)/*прозрачность*/+
8*sizeof(pointer)/*потомки*/+sizeof(byte)/*флаги*/.

При заполнении мира расход памяти стремится к 8/7*L**3, где L=max_size/min_size. Однако, если имеется возможность создавать детали "на лету", то можно сохранять только необходимые уровни деталей, и тогда фактический расход памяти снизится.

Невысокая точность.

В конкретной тестовой реализации неправильно работает отображение прозрачных вокселей - накапливается существенная ошибка. Запустив следующую программу, вы можете сами убедится в значительном расхождении результатов:

#include <stdio.h>

#define TRANSPBITS      7
#define TRANSPONE       (1 << TRANSPBITS)
#define POW     40
#define X       (TRANSPONE-3)

long tmul(long a,long b) {
   a*=b;
   return a>>TRANSPBITS;
} /* tmul */

/* Способ, применяемый при отображении: */
long straight_power(long a,int power) {
   int i;
   long r=TRANSPONE;
   for(i=0;i<power;i++) {
      r=tmul(r,a);
   }
   return r;
} /* straight_power */

/* Способ, применяемый при подсчете усредненных параметров: */
long fast_correct_power(long a,int power) {
   unsigned int mask=0x8000U;
   long r=TRANSPONE;
   while(mask) {
      r=tmul(r,r);
      if(power&mask) r=tmul(r,a);
      mask>>=1;
   }

   return r;

} /* fast_correct_power */

int  main(void) {
   printf("Straight %ld, correct %ld\n",
                    straight_power(X,POW),
                                 fast_correct_power(X,POW)
         );
   return 0;
} /* main */

Этот недостаток можно исправить (за счет использования частично сбалансированного двоичного дерева), однако исправление, скорее всего, повлечет за собой снижение быстродействия. Если быть совсем точным, то здесь требуется дополнительная работа.

Достоинства использования octree

Быстрое отсечение невидимых деталей - если больший куб полностью невидим, значит делить его на меньшие кубы не надо.

Возьмем отрезок 2**N*Focus_len..2**(N+!)*Focus_len. На этом расстоянии будет O(Focus_len) вокселей размером 2**(N+1). Если мир, описываемый восьмидеревом, имеет максимальный линейный размер L, то количество таких отрезков будет log2(L/Focus_len). На экране отображается M=Width*Height лучей. Значит, общая сложность отображения с использование восьмидерева - O(M*log(L))

Встроенный контроль детализации - деление на меньшие объемы прекращается для объема, экранный размер которого составляет от одного до двух пикселов. Если ввести аппроксимацию цвета большего объема, то получится Contionuous Level Of Detail - непрерывность уровня детализации.

Упрощена реализация "молочного тумана" - размывающей свет среды - воксели надо отрисовывать с уменьшенным уровнем детализации. (NB: в тумане предметы кажутся больше, чем они есть на самом деле)

Направление работ

Стоит подумать о более быстром и более правильном механизме отображения.

Восьмидерево, описывающее занимаемый объектами мира объем, позволит описывать любые уровни детализации. При этом более мелкие детали будут создаваться по требованию на основе координат, линейного размера и процедур генерации деталей данного объекта. В этом случае ничего не стоит создавать приближение сферы настолько точно, насколько это нужно.

Восьмидерево освещенности - разумная идея, по-моему.

Как в воксельные картины можно добавить отражение (и преломление)?

Необходимо подумать о более быстром отсечении невидимых деталей. С использованием иерархического z-буфера и(или) карты заслоняющих предметов, a-la мистер Zhang ( здесь ).

Ссылки

www.novalogic.com . Сайт создателей Команчей. Просто так. ;)
Страница Поля Хекберта . На этой странице есть подборка ссылок и библиография по упрощению поверхностей, в том числе и ландшафтов, и моделированию с использованием изменения разрешения модели. Еще есть несколько статей, в которых можно посмотреть создание Level OF Detail для полигональных моделей.
Tech Report: HPL-95-73: Fourier Volume Rendering . Использование преобразования Фурье для отображения объемов.
Visibility Culling using Hierarchical Occlusion Maps , Zhang et al. Интересная статья о сокращении отображаемых деталей, применимая к любому представлению модели.
Рендеринг объемов в реальном времени . Обзорная статья в Open Systems.
A Wavelet-based Multiresolution Polyhedral Object Representation (technical sketch). . Эта статья подвигла меня на размышления, вылившиеся в эту статью.

Приложения

Здесь Исходный текст.

Здесь Выполняемые файлы (для Win32).

Подборка скриншотов, иллюстрирующих статью:

shot000.gif (740 bytes)

Из темноты появляются четыре квадратика вокселей, постепенно приобретая свой "естественный" цвет.

shot001.gif (867 bytes)

Здесь хорошо видно, что квадраты вокселей частично закрывают друг друга. Это сделано для сохранения топологии модели - между элементами поверхности не должно быть просветов.

shot002.gif (3167 bytes)