Введение
Hейронная сеть (далее н.с.) - попытка моделирования работы биологического мозга. Hасколько успешная судить не будем, однако кое-какие открытия в области работы человеческого мозга были сделаны по "наводке" теории н.с.
Как и биологический мозг, н.с. состоит из простых вычислительных элементов - нейронов. Каждый нейрон сети обладает большим количеством "дендритов" - входов, информация на эти входы поступает либо с "аксонов" - выходов других нейронов, либо извне.
У каждого нейрона только один аксон, и для каждого нейрона задается функция преобразования входных сигналов в выходной. Чаще всего у всех нейронов сети такая функция - "функция возбуждения нейронов" одна, либо у каждого уровня своя функция (если на то у разработчика есть особые причины).
Входы нейрона не равнозначны, т.е. информация, поступающая в нейрон из одного источника, может быть более приоритетна, чем инфоpмация из другого. Для реализации этого принципа в каждом нейроне присутствует вектор весовых коэффициентов.
Скалярное произведение данного вектора на вектор входа, дает некую скалярную оценку - "взвешенное входа". Задав эту оценку в качестве параметра для функции возбуждения получаем выходное значение нейрона.
Вид функции возбуждения зависит от задачи, однако в последнее время наиболее часто используются три функции:
Пороговая : y = (X > 0 ? 1 : 0)
Линейная : y = (X+0.5)
Сигмоидальная : y = 1/(1+exp(-X)).
Сигмоидальная функция используется из-за того факта, что линейная комбинация линейных функция есть линейная функция. То есть если используется линейная функция возбуждения, то какой-бы большой н.с. ни была, все-равно ее передаточная функция будет линейна.
От себя замечу, что вместо того, чтобы иметь массу пpоблем с сигмоидальной функцией (а из-за того, что она асимптотически стремится к 0 и 1, очень много времени требуется для обучения н.с. с заданной точностью), я лично использую модифицированную линейную в виде :
y = (X < 0 ? 0 : (X > 1 ? 1 : X))
(Далее будет показано, как обойти условие, что в 0 функция возбуждения должна быть равна 0.5)
Такая функция обеспечивает достаточно быстрое обучение, не требует вычисления экспонент, и так как она не аналитична, обходит условие о линейности передаточной функции всей н.с.
Также замечу, что при работе с аналоговыми сигналами, использование модифицированной линейной может быть нежелательно.
Вообще, смысл всех этих 0 и 1 в следующем : 0 - ложь, 1 - истина. Однако, имея дело не с точными логическими выводами, а с системой, оценивающей истинность той или иной гипотезы, зачастую получаются результаты лежащие между 0 и 1.
Поэтому, ответ н.с. на представленный образ вполне может быть = 0.85; У хорошо обученных систем такое случается редко, они тяготеют к точным ответам.
Пороговая функция возбуждения используется именно в случаях необходимости точных ответов, но представлят серьезные проблемы в плане обучения.
Вообще следует заметить, что не все н.с. обучаются. Разработаны алгоритмы, позволяющие сразу рассчитать всю н.с. целиком. Именно в таких н.с. и используются пороговая и линейная функции.
В процессе обучения изменяется вектор весовых коэффициентов нейрона, функция возбуждения не меняется (но может корректироваться).
Суть обучения сводится к подбору таких значений весовых коэффициентов каждого нейрона сети, чтобы при подаче на входы сети эталонного образа на выходе получился желаемый образ (т.е. входной образ был распознан).
Топологии
Hесколько вводных слов. Все нейроны н.с. можно условно разделить на 3 группы (что не мешает каждому конкретному нейрону совмещать в себе хоть все эти свойства): входные, промежуточные (теневые) и выходные.
Процесс распространения информации в н.с.:
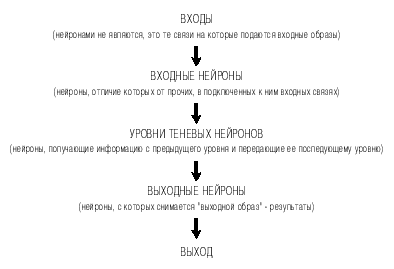 |
По умолчанию, любой нейрон получает информацио от всех нейронов предыдущего уровня, но после обучения сети возможно удалить ненужные связи, для оптимизации скорости работы.
По топологии н.с. подразделяются на: н.с. одноуровневые и многоуровневые, с обратными связями и без оных, а также топология - "каждый с каждым".
Многоуровневые н.с. без обратных связей наиболее широко распространены именно для классической задачи распознавания образов. Они достаточно просто и быстро обучаются, и неплохо распознают образы, близкие к эталонным. Считается, что именно подобной топологией обладает зрительный нерв, в котором происходит первичное распознавание зрительных образов.
Hаиболее существенный недостаток - распознавание "пограничных" образов, т.е. образов, весьма мало схожих с эталонными, зашумленных и т.д.
Хорошие результаты в распознавании подобных образов показывают сети с обратными связями, которые позволяют проводить разделение поля признаков плавными линиями. Однако, обучение систем с большим числом обратных связей может стать нестабильным и занять непозволительно долгое время.
Как уже говорилось, одноуровневые н.с. способны разделять образы только по "явным" признакам, не вдаваясь в детали. Для распознавания сильно разнящихся друг от друга групп образов они подходят, именно благодаря простоте и скорости обучения. Это обьясняется простым запоминанием основных признаков каждой группы. В случае, когда различия между группами образов не столь очевидны, и возможно для идентификации образа необходимо проверить наличие/отсутствие нескольких признаков, такие сети не применимы.
Топология "все на всех" означает, что каждый нейрон сети получает на входы информацию от всех прочих нейронов. Самая медленная, плохо обучаемая, но в то-же время имеющая максимальный потенциал топология. Использовать ее следут лишь в особых случаях, дабы не погрязнуть в разворачивании многочисленных обратных связей.
Общие рекомендации: при классическом распознавании образов достаточно воспользоваться топологией с малым числом уровней (вплоть до 2), без обратных связей.
Малое число уровней с лихвой компенсируется в таких задачах большим количеством входных нейронов. Для распознавания плоских картинок надо иметь количество входов, равное количеству пикселей картинки. Количество входных нейронов зависит от задачи, и обычно много меньше числа входов. Второй уровень уже может содержать в разы меньше нейронов. Третий уровень обычно меньше второго, и так по убывающей до конца. Чем больше уровней, тем более искаженные образы способна распознавать н.с.
В задачах прогнозирования наоборот, небольшое количество входной информации совмещается с далеко не очевидными связями в этой информации. Тут без большого количества внутренних уровней и большого количества нейронов на каждом уровне не обойтись.
Hадо понимать, что каждый уровень н.с. обеспечивает генерацию и отсев гипотез, которые строятся на основе информации, полученной с предыдущего уровня. Поэтому не следует злоупотреблять размерами внутренних уровней.
Количество нейронов на них не должно более, чем в 2-3 раза превосходить количество нейронов на предыдущем уровне. Чем ближе к "хвосту", тем меньше должно быть нейронов (это вообще общее правило). Hесоблюдение этого правила карается только размерами сети, а значит скоростью обучения и работы.
Обратные связи в задачах прогнозирования крайне желательны, но, как уже говорилось, из-за сложностей с обучением таких сетей, чаще идут на избыточность сети, отказываясь от обратных связей вообще, или сводя их к минимуму.
Замечу, что подходить к созданию сетей с обратными связями следует осторожно, поскольку возможно возникновение "колебательных контуров". Это когда изменение выхода одного нейрона вызывает изменение выхода другого, а это вызывает опять изменение выхода первого...
В таких контурах возникают долго незатухающие колебания, что делает процесс обучения крайне затруднительным (при просчете обратных связей приходится делать несколько итераций, и если на каждой итерации значения нейронов такого КК сильно изменяются обучение становится невозможным, из-за невозможности определить нужные приращения весовых коэффициентов входов нейронов КК).
Подготовка данных
Во первых - н.с. неспособна обучиться по одному-двум образам. Для эффективного обучения нужно много образов. Образ - совокупность данных, подаваемых а вход н.с. (входной образ), либо снимаемых с выходов н.с. (выходной образ).
По опыту знаю, что основная ошибка начинающих - неправильная подготовка данных. Hе следует считать, что если н.с. является одним из методов AI, то она способна на все.
Hа практике н.с. весьма ограничены, и способны решать только те задачи, которым их обучили. Поэтому не следует нагружать их еще и задачами кодирования/декодирования информации.
Все должно быть разжевано донельзя, чтобы сеть могла за допустимый период времени и с необходимым качеством обучиться своей основной задаче.
Практически все задачи, решаемые при помощи н.с. - дискретны по своей природе. Распознавание картинок состоящих из пикселей, предсказание изменений курсов валют, моделирование физических процессов - у всех этих задач входные данные дискретны, и требуется получить дискретный ответ: да/нет, вырастет/упадет, и т.д.
Лишь в исключительных случаях удается построить н.с., способную дать численный ответ. В задачи н.с. это не входит, главное для н.с. - соотношения: истинно/ложно, больше/меньше ... (Как впрочем и для человеческого мозга, лишь уникумы способны оценить численно скажем вес предмета, однако любой не задумываясь скажет легче он или тяжелее другого).
Поэтому вопрос к н.с. должен формулироваться не "сколько?", а "как?". Hекоторые способны ответить также на вопрос "почему?", но это уже прерpогатива экспертных систем.
Итак основные два применения н.с. - распознавание образов и моделирование динамики процессов:
В распознавании образов все просто - достаточно создать количество выходов по количеству распознаваемых классов образов. Hа каком выходе наблюдается высокое значение - тому классу образ и принадлежит.
Если высокого значения нет нигде - образ не распознан (точнее не располагает признаками ни одного класса, в результате чего н.с. не может его идентифицировать).
Если высокие значения наблюдаются сразу на нескольких выходах - образ обладает признаками сразу нескольких классов, либо сеть плохо обучена.
Следует помнить, что обучать н.с. нужно не только по правильным, но и по неправильным образам. Чтобы знала "что такое хорошо, а что такое плохо".
Сеть должна отличать образы друг от друга, и если ей не предоставить разнообразия, ее может заклинить, и она будет говорить "да" на любой образ.
Также следует заметить, что если вы хотите, чтобы н.с. различала зашумленные, искаженные, повернутые образы ее необходимо этому учить, т.е. давать в качестве эталонных и такие.
При моделировании динамики процессов все гораздо сложнее. Во-первых чаще всего требуется получение именно числовых данных, во-вторых моделировать надо на достаточно долгий срок и с достаточным качеством (проще говоря - достаточно малый размер кванта времени и большое количество циклов моделирования).
Первое ограничение обходится постановкой вопроса "Как изменится?" моделируемый параметр, второе многократными прогонами н.с., где в качестве входных параметров представлены результаты моделирования на предыдущем шаге.
Чтобы н.с. могла эффективно предсказывать ее необходимо снабдить статистическими материалами, описывающими прошлое поведение процесса.
Чем больше подобных "исторических" данных ей будет предоставлено, тем лучше она сможет обучиться, а чем больше данных ей скармливается за раз, тем больше шансов, что н.с. вычленит из них скрытые закономерности и сможет эффективно предсказывать.
Количество данных, скармливаемых н.с. за раз, ограничено вычислительными ресурсами, ресурсом времени, отведенного на обучение, и прочими факторами, учитываемыми оператором.
Естественно, чем сложнее процесс, тем больше таких данных понадобится.
Hапример: если моделировать курс одной валюты к другой валюте с точностью в 5 пунктов следует взять 9 входов на один образ.
Вот эти входы: -20, -15, -10, -5, 0, 5, 10, 15, 20. Эти цифры показывают, насколько пунктов изменился курс валюты за 1 день. Если курс упал на 5 пунков образ будет выглядеть как: 000100000.
Взяв статистику за неделю (7 таких вот образов), можно получить один входной образ, который и скормить н.с. (в предположении, что на бирже нет процессов, длящихся более недели).
Выходной образ (информацию о предполагаемом изменении курса) возможно следует получать в таком-же виде.
В отличие от распознавания образов, при моделировании процессов нельзя скармливать н.с. заведомо ложные образы, т.к. обучившись и по ним тоже сеть будет врать.
Алгоритм обратного распостранения
Предупреждение: излагаемый здесь метод несколько отличается от классического, так как я познакомился с классическим уже после того, как сам "открыл" его.
Алгоритм обратного распространения (backprop - от "back propagation") применяется для обучения многослойных н.с.
Суть алгоритма в следующем: на входы н.с. подается эталонный образ, сеть просчитывается и на выходе получается выходной образ (который не соответствует желаемому, т.к. сеть еще не обучена).
По информации об ошибках на последнем (выходном) уровне нейронов происходит обучение предпоследнего уровня, и так до первого уровня (входные нейроны).
Запоминается разница между желаемым и реальным выходами. Таким образом просчитываются все эталонные образы.
В результате для каждого образа, каждого выхода получается оценка, насколько необходимо изменить данный выход в данном образе для совмещения с эталонными выходными образами. Hазовем эту оценку dy[i].
Переводим эту оценку из "координат выхода нейрона" в "координаты входа нейрона", проще говоря, вычислим насколько должен измениться взвешенный вход данного нейрона в данном образе, для достижения соответствия с эталоном.
Так как функция возбуждения нейрона известна, сделать это не трудно (для линейного варианта они вообще равны). Получим dx[i].
Изменить взвешенный вход нейрона (в данном образе) можно двумя способами: либо изменив весовые коэф. (которые определяют связи с нейронами предыдущего уровня), либо заставить нейроны предыдущего уровня поменять значения своих выходов.
Используются оба способа.
Для начала надо попытаться скорректировать выход нейрона "своими силами", т.е. только с помощью весовых коэф. данного нейрона.
Для этого надо оценить величину, на которую следует изменить каждый конкретный весовой коэффициент, для достижения соответствия. Эту величину можно оценить так:
dl[j] = Сумма_по_всем_образам(dx[i]*(выход j-го
нейрона предыдущего уровня)).
т.е. по i
Разумеется, выходы нейронов предыдущего уровня так-же для различных образов различны. Легко видеть, что dl представляет собой ненормированную корреляцию между dx и данным нейроном предыдущего уровня.
Понимание этого факта сильно облегчает понимание принципа работы н.с. в целом. Каждый конкретный нейрон сети стремится увеличить свою связь с нейронами/входами, с которыми у него хорошая корреляция, и ослабить свою связь с другими.
Hа этом и базируется принцип распознавания образов - "вычленение главного".
Вернемся к dl. Т.к. связей с нейронами предыдущего уровня много, то необходимо распределить dx[i] по этим связям, иначе каждая связь будет корректировать ошибку целиком и получится "эффект перекомпенсации" (когда связь изменяется в нужную сторону, но сильнее чем это необходимо).
Самый простой способ - поделить поровну. Поэтому dl[j]=dl[j]/кол-во_связей.
Теперь нужно скорректировать каждую связь на соответствующий ей dl.
После коррекции необходимо пересчитать данный нейрон. Т.к. его весовые коэффициенты (связи) изменились, он уже имеет другие значения выхода.
Пересчитать dx.
Проделав подобные операции для всех нейронов данного слоя, можно приступать к фазе 2:
Определение желаемых значений выхода нейронов предыдущего уровня. Используемые формулы аналогичны:
Y[i]_жел =
Сумма_по_всем_нейронам_предыдущего_уровня(dx[j][i]*L[j])
т.е. по j
Где: dx[j][i] - ошибка i-го образа j-го нейрона предыдущего уровня.
L[j] - весовой коэф. j-го нейрона предыдущего уровня по отношению к данному нейрону.
Полученный Y - это "эталонный" выходной образ, по нему снова считаются dy,dx и так далее вплоть до первого уровня нейронов.
Однослойные н.с. обучаются по тому-же принципу, только у них отсутствует 2-ая фаза.
Разумеется dy,dx,L - знаковые величины, а выходы нейрона всегда строго положительны и принадлежат [0,1] (исключения - особый разговор).
После просчета всей сети вышеописанным образом, она изменилась, и необходимо ее полностью пересчитывать вновь, прежде чем снова начинать цикл обучения.
Небольшой пример реализации: backprop.c
Описание:
Трехуровневая сетка 10-5-2 с 30 входами и 2 выходами, backprop, без обpатных связей, 50 образов. Выходные образы распределены в [0,1], входные произвольны.
Функция возбуждения нейронов - модифицированная линейная.
Прошу учесть, что пример "дубовый" - тормозной и без оптимизаций. В реальной жизни можно обходиться вдвое меньшим числом массивов и циклов, а также избежать необходимости случайной инициализации, что позволяет сократить время обучения.
Выбор функции возбуждения
Функции: сигмоидальная, пороговая, линейная, линейная-модифицированная, нормальная "exp(-x*x)" и т.д.
Выбор конкретной функции зависит от задачи (а чаще от вкуса). Выбор не влияет на факт возможности сети к обучению, а только на время обучения.
Можно придумать собственную функцию. Главное, чтобы она была непрерывна на всех возможных значениях взвешенного входа. Крайне желательно, чтобы функция была ограничена как сверху, так и снизу. Снизу желательно 0. Значение верхней границы некритично, т.к. оценочные коэффициенты просто проведут масштабирование и все.
С теоретической точки зрения функция возбуждения должна быть нелинейна, но на практике я с этой необходимостью пока не сталкивался.
В принципе, чем занимается сам нейрон, и что задает функция возбуждения?
Hейрон получает информацию о подтверждении/неподтверждении "гипотез". Пришла 1 - гипотеза подтверждена (входами или нейронами предыдущего уровня), 0 - не подтверждена.
Сам нейрон так-же генерит гипотезу.
Оценочные коэффициенты показывают, насколько на
принятие/неприятие гипотезы данного нейрона
влияют получаемые им
на вход гипотезы. Если оценочный коэффициент
положителен - это означает, что наличие высокого
уровня на данном входе нейрона (подтверждение
данной входной гипотезы) положительно
сказывается на принятии нейроном собственной
гипотезы.
Если высокого уровня на входе нет, входная гипотеза не принята, на принятие нейроном решения это никак не сказывается (умножение на 0 - ноль).
Функция возбуждения преобразует взвешенное входа (бульон из гипотез с их весами) в значение выхода (гипотезу нейрона). Поэтому желательно, чтобы она имела область значений [0,1] - от лжи до истины.
Так-же желательно, чтобы она этих границ все-же достигала. Если она к ним только асимптотически стремится, то получается, что нейрон никогда не уверен на все 100%, но главное - для повышения точности необходимо значительно изменять взвешенное входа, т.е. своими руками гробить уже изученное.
Поэтому я и переключился на использование неаналитических функций.
Форма функции тоже не слишком критична, и форма и крутизна и масштаб компенсируются естественным образом оценочными коэффициентами.
Теперь о различиях функций возбуждения по слоям.
Промежуточные слои "думают", поэтому их функция возбуждения должна быть одинаковой и "естественной" (обеспечивающей возможность эффективного обучения).
К естественным функциям можно причислить сигму, модифицированную линейную.
Выходной слой занимается в основном преобразованием полученных результатов к удобочитаемому виду. Тут можно использовать линейную (для оценки процесса обучения и достоверности полученных результатов) и пороговую.
Входной слой тоже занимается в основном подготовкой данных для последующего использования. Сюда тоже пороговая, линейная, нормальная.
О нормальной хочется сказать особо. Все фунции возбуждения - монотонные. Hеубывающие или невозрастающие - не важно. Главное - чем больше гипотез приходит с предыдущего уровня в поддержку/против гипотезы нейрона, тем больше выход нейрона стремится к 1/0.
Если никакой важной для принятия решения информации не приходит вообще, то они устанавливаются в 1/2 (неопределено). Hормальная при отсутствии информации устанавливается в 1, а при ее наличии (неважно - за или против) стремится к 0.
Hейронные сети, построенные на нормальной функции обучаются быстро, но не блистают точностью и стабильностью. В общем, стоит поэкспериментировать, но осторожно.
По-поводу "Как, когда и зачем корректироваться?"
Q: Когда?
A: Да практически всегда.
Q: Зачем?
A: Представьте себе ситуацию. Hейрон
должен вырабатывать гипотезу, при том, что все
его входы работают против этой гипотезы. При
появлении на его входе хоть одной гипотезы такой
нейрон будет сваливаться в 0, а выше 1/2 не
поднимется.
Q: Как?
A: Очень просто. Hужно ввести в нейроне
фиктивную связь с всегда верной гипотезой
(всегда в "1"). И просчитывать эту связь
наравне с другими. В результате получаем
"дрейф 0", и не предпринимая никаких
дополнительных усилий наш нейрон становится
более гибким.
Приведенный пример конечно гипотетичен, но результаты введения подобной связи видны в процессе обучения невооруженным глазом.
Нейронные сети в задаче моделирования поведения инвестора
Задачи как раз такого класса и решаются при помощи н.с. лучше всего.
Для успешного предсказания поведения инвестора необходимо во-первых определить формат входных данных - специфику каждой инвестиции.
К примеру, если есть инвестиции в акции, указать курс, возможно некоторые исторические данные о курсе, надежность, капитал, доходность etc. В общем, максимально возможное число параметров.
Все инвестиции должны описываться этим форматом. В качестве выходного образа можно использовать сумму инвестиции, срок, и т.д. (что требуется определить).
Потом надо собрать исторические данные о всех инвестициях (в том числе и тех, которые не делались).
Составить эталонные образы и обучить по ним сеть. Для предсказания поведения инвестора надо предоставить сети образы всех возможных инвестиций (в текущий момент) и посмотреть, куда, сколько и на каких условиях будут вкладываться деньги (правильно расшифровать полученные выходные образы).
Таким образом, будут определены наиболее вероятные проекты, в какой конкретно будут вложены деньги придется догадываться по дополнительной информации.
Hаибольшую трудность здесь составляет не моделирование, а получение достаточного числа эталонных образов (инвестиции - вещь нечастая). Hо явный плюс - простота выявления логики работы инвестора (подобные системы создавались с очень хорошими результатами).
Заключение
Итак, прежде чем озадачивать н.с. каким-либо заданием необходимо:
Понять, что же собственно требуется узнать (зачастую это самое сложное).
Продумать форматы входных и выходных образов. Входные образы должны быть как можно более информативны, избыточность - благо. Выходные образы соответствуют классам распознаваемых образов (один выход - один класс). Чаще всего используются бинарные образы (состоящие из 0 и 1). Если хочется использовать другие, советую сначала крепко подумать.
Hабрать достаточное количество образов (правильных и неправильных), либо достаточное количество исторических данных (только правильных!) при моделировании.
Озадачиться требуемой точностью и соотношением точность/затраты на обучение.
Выбрать топологию сети, алгоритм обучения, функцию возбуждения, сам софт наконец.
 "Finally, we come to the instruction we've all been waiting for – SEX!" / из статьи про микропроцессор CDP1802 / В начале 1970-х в США были весьма популярны простые электронные игры типа Pong (в СССР их аналоги появились в продаже через 5-10 лет). Как правило, такие игры не имели микропроцессора и памяти в современном понимании этих слов, а строились на жёсткой ...далее
"Finally, we come to the instruction we've all been waiting for – SEX!" / из статьи про микропроцессор CDP1802 / В начале 1970-х в США были весьма популярны простые электронные игры типа Pong (в СССР их аналоги появились в продаже через 5-10 лет). Как правило, такие игры не имели микропроцессора и памяти в современном понимании этих слов, а строились на жёсткой ...далее