|
|
Вообще говоря, лучше всего немного почитать любую книжку по линейной алгебре. Здесь будет только краткий рассказ о 3D преобразованиях, о том, как их делать с помощью матриц, и о том, что же такое матрицы и как с ними работать. Введем несколько терминов. n-мерный вектор, он же вектор размерности n, он же вектор размера n: упорядоченный набор n действительных чисел. Вообще говоря, практически то же самое, что и обычный 1D-массив. Матрица размера m на n (будет обозначаться как m*n, mxn): таблица размера m на n, в каждой клетке которой - действительное число. Это уже 2D-массив. Всего лишь. Вот пример матрицы 3x3: [ 15 y*z 0.6 ] [ 7 -3 91 ] [ sin(x) 0.123 exp(t) ] Займемся определением операций над векторами и матрицами. Вектор будем записывать в столбик и рассматривать его как матрицу размера n*1. Операция скалярного произведения векторов: определена для двух векторов одинаковых размеров. Результат есть число, равное сумме произведений соответствующих элементов векторов. Пример: [ 1 ] [ 4 ] [ 2 ] * [ 5 ] = 1*4 + 2*5 + 3*6 = 32 [ 3 ] [ 6 ] Операция векторного произведения: определена для (n-1) вектора одинакового размера n. Результат - вектор, причем, что интересно, перпендикулярный всем множителям. Результат меняется от перестановки мест множителей!!! Формально определяется как определитель матрицы, первая строка которой есть все базисные вектора, а все последующие - соответствующие координаты всех множителей. Поскольку нам она будет требоваться только для 3D пространства, мы определим векторное произведение двух 3D векторов явно:
[ Ax ] [ Bx ] | i j k | [ Ay*Bz-Az*By ]
AxB = [ Ay ] x [ By ] = | Ax Ay Az | = [ Az*Bx-Ax*Bz ]
[ Az ] [ Bz ] | Bx By Bz | [ Ax*By-Ay*Bx ]
Операция сложения двух матриц: определена для матриц одинаковых размеров. Каждый элемент суммы (то есть, каждое число в таблице) равняется сумме соответствующих элементов слагаемых-матриц. Пример: [ 1 x 500 ] [ 8 a 3 ] [ 9 a+x 503 ] [ 2 y 600 ] + [ 9 b 2 ] = [ 11 b+y 602 ] [ 3 z 700 ] [ 10 c 1 ] [ 13 c+z 701 ] Операция умножения матрицы на число: определена для любой матрицы и любого числа; каждый элемент результата равняется произведению соответствующего элемента матрицы-множителя и числа-множителя. Операция умножения двух матриц: определена для двух матриц таких размеров a*b и c*d, что b = c. Например, если b = c, но a != d, то при перестановке множителей операция будет вообще не определена. Результатом умножения матрицы A размером a*b на матрицу B размером b*d будет матрица C размером a*d, в которой элемент, стоящий в строке i и столбце j, равен произведению строки i матрицы A на столбец j матрицы B. Произведение строки на столбец определяется как сумма произведений соответствующих элементов строки и столбца. Чтобы было хоть чуть-чуть понятно, пример умножения строки на столбец (они должны быть равной длины, кстати; поэтому и такие ограничения на размеры матриц):
[ 4 ]
[ 1 2 3 ] * [ 5 ] = 1*4 + 2*5 + 3*6 = 32
[ 6 ]
А чтобы перемножить две матрицы, надо эту операцию проделать для каждого элемента. Вот пример: [ 1 2 3 ] [ 0 3 ] [ 1*0+2*1+3*2 1*3+2*4+3*5 ] [ 4 5 6 ] * [ 1 4 ] = [ 4*0+5*1+6*2 4*3+5*4+6*5 ] = ... [ 7 8 9 ] [ 2 5 ] [ 7*0+8*1+9*2 7*3+8*4+9*5 ] Умножение и сложение матриц обладают почти тем же набором свойств, что и обычные числа, хотя некоторые привычные свойства не выполняются (например, A*B != B*A); нам на самом деле понадобится знать, что произведение вида A*B*C*D*... не зависит от того, как расставить скобки. Или, если угодно, что A*(B*C) = (A*B)*C. Теперь забудем об этом на некоторое время и перейдем к преобразованиям. Любое движение (то есть преобразование пространства, сохраняющее расстояние между точками) в трехмерном пространстве, согласно теореме Шаля, может быть представлено в виде суперпозиции поворота и параллельного переноса, то есть последовательного выполнения поворота и параллельного переноса. Именно поэтому основная часть информация о поведении объекта - это его смещение, ось поворота и угол поворота. И именно поэтому нам достаточно знать, как сделать два преобразования - перенос и поворот. Перенос точки (кстати, точки будут также рассматриваться как вектора с началом в начале координат и концом в собственно точке) с координатами (x,y,z) на вектор (dx,dy,dz) делается простым сложением всех координат. То есть результат - это (x+dx,y+dy,z+dz). Как бы сложили вектор-точку и вектор-перенос. Поворот - занятие уже более интересное. Но тоже простое. Рассмотрим для примера поворот точки (x,y,z) относительно оси z. В этом случае z не меняется вообще, а (x,y) меняются так же, как и при 2D повороте относительно начала координат. Посмотрим, какие будут координаты у точки A' - результата поворота A(x,y) на угол alpha. 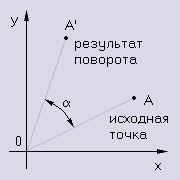 Пусть r = sqrt(x*x+y*y). Пусть угол AOx равен phi, тогда из рисунка видно, что cos(phi) = x/r, sin(phi) = y/r. Угол A'OA равен по условию alpha. Отсюда
x' = r*cos(alpha+phi) = r*(cos(alpha)*cos(phi)-sin(alpha)*sin(phi)) =
y' = r*sin(alpha+phi) = r*(cos(alpha)*sin(phi)+sin(alpha)*cos(phi)) = Для трехмерного случая, таким образом x' = x*cos(alpha)-y*sin(alpha) Аналогичные формулы получатся и для других осей поворота (то есть Ox, Oy). Поворот относительно произвольной оси, проходящей через начало координат, можно сделать с помощью этих поворотов - сделать поворот относительно Ox так, чтобы ось поворота стала перпендикулярна Oy, затем поворот относительно Oy так, чтобы ось поворота совпала с Oz, сделать собственно поворот, а затем обратные повороты относительно Oy и Ox. Можно даже вывести формулы для такого поворота и убедиться в том, что они очень громоздкие. Вспомним о матрицах и векторах и внимательно посмотрим на выведенные формулы для поворота. Можно заметить, что [ x' ] = [ cos(alpha) -sin(alpha) 0 ] [ x ] [ y' ] = [ sin(alpha) cos(alpha) 0 ] [ y ] [ z' ] = [ 0 0 1 ] [ z ] То есть поворот на угол alpha задается одной и той же матрицей, и с помощью этой матрицы (умножая ее на вектор-точку) можно получить координаты повернутой точки. Пока никакого выигрыша не видно - здесь умножение матрицы на вектор требует больше операций, чем расчет x' и y' по формулам. Удобство матриц для нас заключается как раз в свойстве A*(B*C) = (A*B)*C. Пусть мы делаем несколько поворотов подряд, например, пять (как раз столько, сколько надо для поворота относительно произвольной оси), и пусть они задаюся матрицами A, B, C, D, E (A - матрица самого первого поворота, E - последнего). Тогда для вектора p мы получаем p' = E*(D*(C*(B*(A*p)))) = E*D*C*B*A*p = (E*D*C*B*A)*p = (E*(D*(C*(B*A))))*p = T*p, где T = (E*(D*(C*(B*A)))) матрица преобразования, являющегося комбинацией пяти поворотов. Посчитав один раз эту матрицу, можно в дальнейшем без проблем применить довольно сложное преобразование из пяти поворотов к любому вектору с помощью всего одного умножения матрицы на вектор. Таким образом, можно задать любой поворот матрицей, и любая комбинация поворотов также будет задаваться матрицей, которую можно довольно легко посчитать. Но есть еще параллельный перенос, есть еще масштабирование. Что делать с ними? На самом деле, эти преобразования тоже легко записываются в виде матриц. Только вместо матриц 3x3 и 3-мерных векторов используются так называемые однородные 4-мерные координаты и матрицы 4x4. При этом вместо векторов вида [ x ] [ y ] [ z ] используются вектора вида [ x ] [ y ] [ z ] [ 1 ] а вместо произвольных матриц 3x3 используются матрицы 4x4 такого вида: [ a b c d ] [ e f g h ] [ i j k l ] [ 0 0 0 1 ] Видно, что если d = h = l = 0, то в результате применения всех операций получается то же самое, что и для матриц 3x3. Матрица параллельного переноса теперь определяется как [ 1 0 0 dx ] [ 0 1 0 dy ] [ 0 0 1 dz ] [ 0 0 0 1 ] Матрицу масштабирования можно определить и для матриц 3x3, и для матриц 4x4:
[ kx 0 0 ] [ kx 0 0 0 ]
[ 0 ky 0 ] или [ 0 ky 0 0 ]
[ 0 0 kz ] [ 0 0 kz 0 ]
[ 0 0 0 1 ]
где kx, ky, kz - коэффициенты масштабирования по соответствующим осям. Таким образом, получаем следующее. Любое нужное нам преобразование пространства можно задать матрицей 4x4 определенной структуры, разной для разных преобразований. Результат последовательного выполнений нескольких преобразований совпадает с результатом одного преобразования T, которое также задается матрицей 4x4, вычисляемой как произведение матриц всех этих преобразований. Важен порядок умножения, так как A*B != B*A. Результат применения преобразования T к вектору [ x y z ] считается как результат умножения матрицы T на вектор [ x y z 1 ]. Вот и все. Осталось только на примере показать, почему A*B != B*A. Пусть A - матрица переноса, B - поворота. Если мы сначала перенесем объект, а потом повернем относительно центра координат (это будет B*A), получим далеко не то, что будет, если сначала объект повернуть, а потом перенести (это уже A*B). |
 |
|